2020-11-05 周报#11 刘潘

#I. Task achieved last week

  • 《MotionSqueeze: Neural Motion Feature Learning for Video Understanding》重新精读了一遍并整理了笔记。
  • 添加了MS模块的网络，准确率分别提高了0.6%和0.8%。
  • 《Temporal Interlacing Network》网络的效果不好，准确率大概降低了0.8%，设计的模块可能和我现有的网络有所冲突。

#II. Reports

#MotionSqueeze: Neural Motion Feature Learning for Video Understanding

主要的创新点是MS module，它把这个结构插入到了ResNet的网络中间，具体来说在layer2之后，layer3之前。

结构图

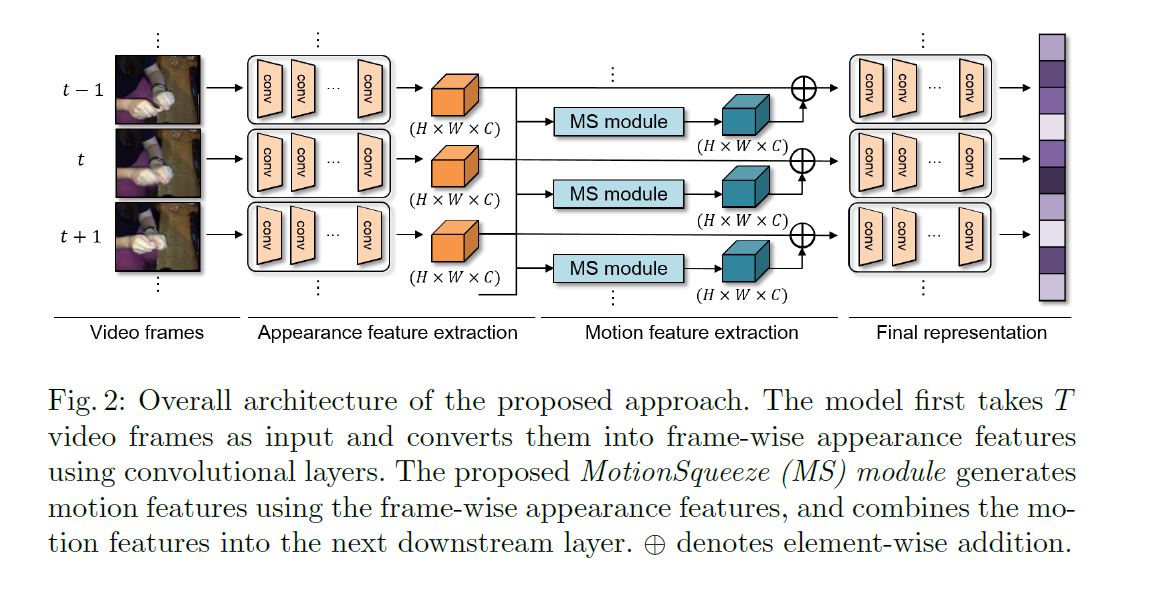
逻辑上如下图所示，道理上说得很清楚，首先进行关联性计算，就是为了判断当前的点可能会位移到什么位置，即什么位置的点最有可能是由当前的点位移过去的。

然后通过估计上的点，计算偏移。

最后计算特征转换。（这个其实我没太理解）

结构图

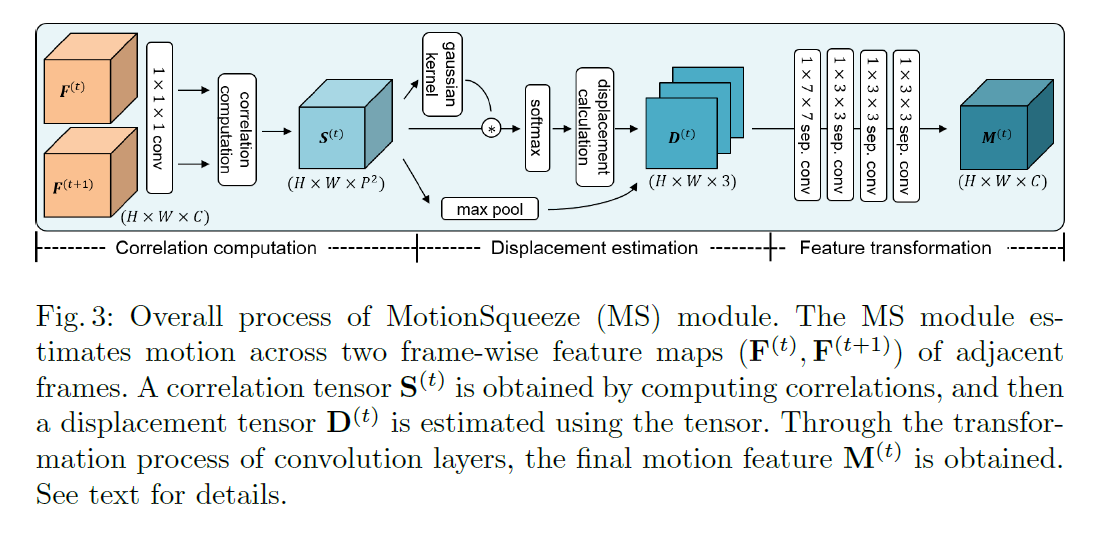
#相关工作

对于一个视频来说，动作是最显著的特征，动作模型提取得好，识别的准确率就会提高。

卷积在捕获平移等变化的模型上具备有效性，但是对相对运动的物体上建模就很难让人感到满意。

convolution is effective in capturing translation-equivariant patterns but not in modeling relative movement of objects

论文的主要工作放在如何学习动作特征上。

we focus on efficient learning of motion features.

一些现有的研究方向进展：

  1. 有一些在推理部分不需要光流输入，但是训练仍然需要的。
  2. 通过计算特征的时空梯度来表征动作特征。
  3. 提出了一种卷积模块，通过在外观特征之间进行空间移动和减法运算来提取运动特征。
  4. 计算卷积神经网络中间层的特征层光流，虽然效果很好，但是需要很高的计算量，因为在网络中间层进行操作。

光流估计方法：

  1. 对特征图构建张量，并对张量进行回归。
  2. 通过堆叠的特征层来进行粗略的光流估计。

不过这些方法都需要光流图做ground-truth。

最近的一些相关工作：

  1. 利用连续帧的特征图之间的相关信息来代替光学图像。不过这个完整模型的大小与双流网络相当。
  2. 提出correspondences proposal模块来学习视频间的联系。

#MS模块

主要分为三个步骤相关性计算（correlation computation）、位移估计（displacement estimation）和特征变换（feature transformation）。

#相关性计算

定义给定的某一个特征层的输入特征图$\mathbf{F}^{(t)}$和$\mathbf{F}^{(t+1)}$，$\mathbf{F}$的大小为：

$$
\mathbf{F} \in \mathbb{R}^{C \times H \times W}
$$

对于某一个位置$\mathbf{x}$和位移$\mathbf{p}$的相关性可以通过下列公式得到：

$$ s(\mathbf{x},\mathbf{p},t)=\mathbf{F}^{(t)}_{\mathbf{x}} \cdot \mathbf{F}^{(t+1)}_{\mathbf{x}+\mathbf{p}} $$

$\cdot$代表点积。

为了保证计算效率，同时也可以从经验中得到其实一个位置的运动相对不会很大（鉴于数据集是25帧-56帧不等，其实也还是蛮大的）[1]，$\mathbf{p}$有一个范围$\mathbf{p}\in[-k,k]^2$。

最终相关性结果为：

$$
\mathbf{S}^{(t)} \in \mathbb{R}^{H \times W \times P^2}, P=2k+1
$$

这个计算量与$P^2$个$1 \times 1$的卷积核计算量相当，整个视频的FLOPs为$T H W C P^2$。

在计算相关性之前，先在前面进行一次卷积操作，目的是为了对这些特征通道进行加权，进而来学习相关的视觉联系。

We apply a convolution layer before computing correlations, which learns to weight informative feature channels for learning visual correspondences.

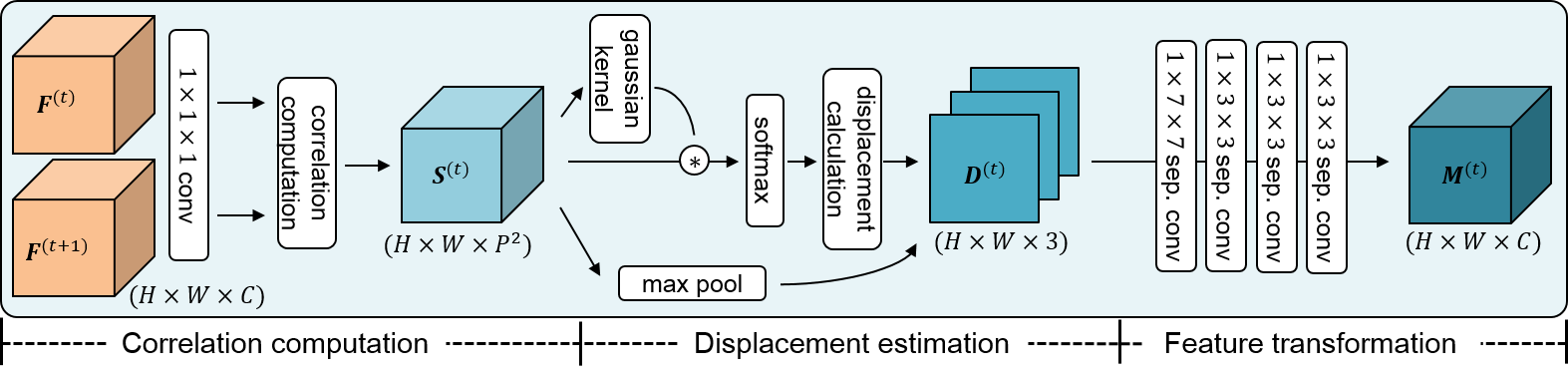
MS结构图

#位移估计

在前面，我们已经得到了某个点，与这个点在下一帧图像中周围点的相关性张量，然后就可以找出这里面相关性最大的点做位移估计。

最简单且最有效地方法当然是直接用$\mathrm{argmax}_{\mathbf{p}}s(\mathbf{x},\mathbf{p},t)$来计算，但是这个方法是不可微的，所以用一个替代方法：soft-argmax，定义如下：

$$
d(\mathbf{x},t) = \sum_{\mathbf{p}} \frac{\exp(s(\mathbf{x},\mathbf{p},t))}{\sum_{\mathbf{p}’}{\exp(s(\mathbf{x},\mathbf{p}’,t))}} \mathbf{p}.
$$

但是这个方法会对周围的噪点比较敏感，因为他受所有的点的值影响，解决方法是：kernel-soft-argmax，思路是对非中心点进行抑制，所以得到的结果大部分会来自中心点，及周围相关的点：

$$
d(\mathbf{x},t) = \sum_{\mathbf{p}} \frac{\exp(g(\mathbf{x},\mathbf{p},t)s(\mathbf{x},\mathbf{p},t) / \tau )}{\sum_{\mathbf{p}’}{\exp( g(\mathbf{x},\mathbf{p}’,t) s(\mathbf{x},\mathbf{p}’,t) / \tau )}} \mathbf{p},
$$

$$
g(\mathbf{x},\mathbf{p},t) = \frac{1}{\sqrt{2\pi}\sigma}\exp(\frac{\mathbf{p}-\mathrm{argmax}_{\mathbf{p}}s(\mathbf{x},\mathbf{p},t)}{\sigma^{2}})
$$

根据经验，令$\sigma=5$。$\tau$是一个温度因子，用来调节softmax的分布，随着$\tau$的下降，softmax表现为argmax，令$\tau=0.01$。

除此之外，使用相关置信度图作为辅助运动信息，求解方法是对每个位置点$\mathbf{x}$进行最大池化：

$$
s^{*}(\mathbf{x},t) =\max_{\mathbf{p}}s(\mathbf{x},\mathbf{p},t)
$$

$$
\mathbf{S}^* \in \mathbb{R}^{H \times W \times 1}
$$

论文里说位移估计最后出来有两个通道，但是我目前还不知道为什么是双通道，待到看代码应该可以知道。

然后把两通道和上面的单通道合并，得到位移估计张量：

$$
\mathbf{D}^{(t)} \in \mathbb{R}^{H \times W \times 3}
$$

MS结构图

#特征变换

用四层卷积卷，depth-wise separable convolution，因为上述特征都是通过两帧相减得到的，所以最后会少一个特征，论文直接令$\mathbf{M}^{(T)}=\mathbf{M}^{(T-1)}$，$\mathbf{M}^{(T)}$是上一步的$\mathbf{D}^{(T)}$卷积得到的。

经过卷积操作，也恢复成了原来的尺寸：

$$
\mathbf{D}^{(t)} \in \mathbb{R}^{H \times W \times C}
$$

MS结构图

最终的结果会加回到原来的特征图上，论文通过做实验发现这样效果最好：

$$
\mathbf{F}’^{(t)} =\mathbf{F}^{(t)} + \mathbf{M}^{(t)}
$$

网络图

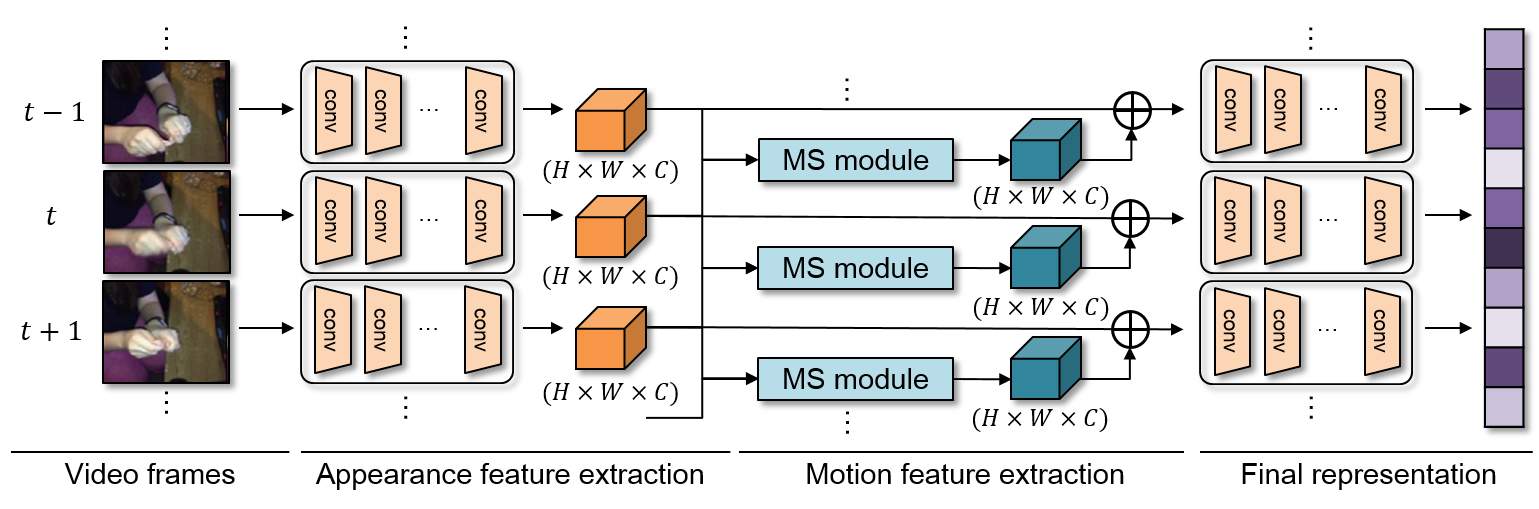
#详细代码

1
2
3
4
5
6
7
8
9
10
x = self.layer1(x)                             
x = self.layer2(x)          

# Flow 
flow_1, match_v = self.flow_computation(x, temperature=temperature)
x = self.flow_refinement(flow_1, x, match_v)
# EndFlow 

x = self.layer3(x)                           
x = self.layer4(x)

首先是代码入口，代码就是在ResNet的层之间添加的，具体的是在layer2和layer3之间。一共有两个方法，一共是上面说的MS的计算，即flow_computation，这里出来的结果是上面说的$\mathbf{D}^{(t)}$，上面说过$\mathbf{D}^{(t)}$有三个通道，flow_1是前两个光流通道，match_v是第三个的辅助运动信息，即$\mathbf{S}^*$。第二个是MS的几个卷积层+最终的融合，就是从$\mathbf{D}^{(t)}$到$\mathbf{M}^{(t)}$再到$\mathbf{F}'^{(t)}$的过程，即flow_refinement。

然后看一下flow_computation方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def flow_computation(self, x, pos=2, temperature=100):
	
	x = self.chnl_reduction(x)
	# chnl_reduction 源码如下，主要做的操作是降低通道数
	# self.chnl_reduction = nn.Sequential(
	#     nn.Conv2d(128*block.expansion, 64, kernel_size=1, stride=1, padding=0, bias=False),
	#     nn.BatchNorm2d(64),
	#     nn.ReLU(inplace=True)
	# )
	
	size = x.size()               
	x = x.view((-1, self.num_segments) + size[1:])        # N T C H W
	x = x.permute(0,2,1,3,4).contiguous() # B C T H W   
					
	# match to flow            
	k = 1            
	temperature = temperature                    
	b,c,t,h,w = x.size()            
	t = t-1         

	x_pre = x[:,:,:-1].permute(0,2,1,3,4).contiguous().view(-1,c,h,w)
	x_post = x[:,:,1:].permute(0,2,1,3,4).contiguous().view(-1,c,h,w)
		
	match = self.matching_layer(x_pre, x_post)    # (B*T-1*group, H*W, H*W)          
	u, v, confidence = self.match_to_flow_soft(match, k, h, w, temperature)
	flow = tr.cat([u,v], dim=1).view(-1, 2*k, h, w)  #  (b, 2, h, w)            
			
	# backward flow
#             match2 = self.matching_layer(x_post, x_pre)
#             u_2, v_2, confidence_2 = self.match_to_flow_soft(match2, k, h, w,temperature)       
#             flow_2 = tr.cat([u_2,v_2],dim=1).view(-1,2, h, w)   

	return flow, confidence

首先进行了降低通道数的操作，然后对于不同 $t$ 时刻的特征图，进行matching_layer操作，得到match张量，对应论文中的$\mathbf{S}^{(t)}$，代码如下：

1
2
3
4
5
6
7
8
feature1 = self.L2normalize(feature1)
feature2 = self.L2normalize(feature2)
b, c, h1, w1 = feature1.size()
b, c, h2, w2 = feature2.size()
corr = self.correlation_sampler(feature1, feature2)
corr = corr.view(b, self.patch * self.patch, h1* w1) # Channel : target // Spatial grid : source
corr = self.relu(corr)
return corr

直接写了一个forward方法，correlation_sampler调用的是一个第三方的库：

1
self.correlation_sampler = SpatialCorrelationSampler(ks, patch, stride, pad, patch_dilation)

总得来说就是求相关性的。

然后是match_to_flow_soft方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def match_to_flow_soft(self, match, k, h,w, temperature=1, mode='softmax'):        
	b, c , s = match.size()     
	idx = tr.arange(h*w, dtype=tr.float32).to('cuda')
	idx_x = idx % w
	idx_x = idx_x.repeat(b,k,1).to('cuda')
	idx_y = tr.floor(idx / w)   
	idx_y = idx_y.repeat(b,k,1).to('cuda')

	soft_idx_x = idx_x[:,:1]
	soft_idx_y = idx_y[:,:1]
	displacement = (self.patch-1)/2
	
	topk_value, topk_idx = tr.topk(match, k, dim=1)    # (B*T-1, k, H*W)
	topk_value = topk_value.view(-1,k,h,w)
	
	match = self.apply_gaussian_kernel(match, h, w, self.patch, sigma=5)
	match = match*temperature
	match_pre = self.soft_argmax(match)
	smax = match_pre           
	smax = smax.view(b,self.patch,self.patch,h,w)
	x_kernel = tr.arange(-displacement*self.patch_dilation, displacement*self.patch_dilation+1, step=self.patch_dilation, dtype=tr.float).to('cuda')
	y_kernel = tr.arange(-displacement*self.patch_dilation, displacement*self.patch_dilation+1, step=self.patch_dilation, dtype=tr.float).to('cuda')
	x_mult = x_kernel.expand(b,self.patch).view(b,self.patch,1,1)
	y_mult = y_kernel.expand(b,self.patch).view(b,self.patch,1,1)
		
	smax_x = smax.sum(dim=1, keepdim=False) #(b,w=k,h,w)
	smax_y = smax.sum(dim=2, keepdim=False) #(b,h=k,h,w)
	flow_x = (smax_x*x_mult).sum(dim=1, keepdim=True).view(-1,1,h*w) # (b,1,h,w)
	flow_y = (smax_y*y_mult).sum(dim=1, keepdim=True).view(-1,1,h*w) # (b,1,h,w)    

	flow_x = (flow_x / (self.patch_dilation * displacement))
	flow_y = (flow_y / (self.patch_dilation * displacement))
		
	return flow_x, flow_y, topk_value

这里就可以解释上面的疑问了，为什么匹配出来的通道数是2，就是和光流一样的原因，一个是x方向上的，一个是y方向上的。

  1. 这第二句话是我自己加的，论文里只是为了保证计算效率。 ↩︎