#用人工神经网络求解旅行商(TSP)问题

#问题描述

旅行商问题(Travelling Salesman Problem, 简记TSP, 亦称货郎担问题): 设有34个城市及其对应的经纬度坐标, 则问题是要找出遍访每个城市恰好一次的一条回路并使其路径长度为最短.

#算法设计

Hopfield神经网络是一种单层互相全连接的反馈型神经网络。每个神经元既是输入也是输出，网络中的每一个神经元都将自己的输出通过连接权传送给所有其它神经元，同时又都接收所有其它神经元传递过来的信息。即：网络中的神经元在t时刻的输出状态实际上间接地与自己t-1时刻的输出状态有关。神经元之间互连接，所以得到的权重矩阵将是对称矩阵。
同时，Hopfield神经网络成功引入能量函数的概念，使网络运行地稳定性判断有了可靠依据。基本的Hopfield神经网络是一个由非线性元件构成的全连接型单层递归系统。其状态变化可以用差分方程来表示。递归型网络的一个重要特点就是它具有稳定状态, 当网络达到稳定状态的时候，也就是它的能量函数达到最小的时候。这里的能量函数不是物理意义上的能量函数，而是在表达形式上与物理意义上的能量概念一致，即它表征网络状态的变化趋势，并可以依据Hopfield网络模型的工作运行规则不断地进行状态变化，最终能够到达具有某个极小值的目标函数。网络收敛就是指能量函数达到极小值。
如果把一个最优化在着递归信号，网络的状态是随时间的变化而变化的，其运动轨迹必然存在着稳定性的问题。这就是递归网络与前向网络在网络性能分析上最大的区别之一在使用递归网络时，必须对其稳定性进行专门的分析与讨论，合理选择网络的参数变化范围，才能确保递归网络的正常工作。
Hopfield神经网络模型有离散型和连续性两种，离散型适用于联想记忆，连续性适合处理优化问题。^[1]

将TSP问题映射为神经网络动力系统可用以下步骤完成：

将TSP问题的每一条可能路径用一换位矩阵表示，并给出相应的距离表示试；
将TSP问题的换位阵集合与由N个神经元构成的神经元阵列相对应；每一条路径所对应的换位阵的各元素与相应的神经元稳态输出对应；
找出一反应TSP约束优化问题的能连函数E；
求出使E取极小值的神经网络连接权重矩阵和偏置参数。

#TSP的能量函数E

$$ \begin{aligned} E = & \frac{A}{2}\sum^n_{x=1}\sum^n_{i=1}\sum^n_{j \ne 1}v_{xi}v_{xj} + \frac{B}{2}\sum^n_{i=1}\sum^n_{x=1}\sum^n_{y \ne x}v_{xi}v_{yi} \\ & + \frac{C}{2}(\sum^n_{x=1}\sum^n_{i=1}v_{xi}-n)^2 + \frac{D}{2}\sum^n_{x=1}\sum^n_{y \ne x}\sum^n_{i=1}d_{xy}d_{xi}(v_{y,i+1}+v_{y,i-1}) \end{aligned} \tag{1} $$

其中参数$ABCD$称为权值，前三项是满足TSP置换矩阵的约束条件，最后一项包含优化目标函数项.

#改进的TSP的能量函数E

$$ \begin{aligned} E = & \frac{A}{2}\sum^n_{x=1}(\sum^n_{i=1}v_{xi}-1)^2+ \frac{A}{2}\sum^n_{i=1}(\sum^n_{x=1}v_{xi}-1)^2 \\ & + \frac{D}{2}\sum^n_{x=1}\sum^n_{y=1}\sum^n_{i=1}v_{xi}d_{xy}v_{y,i+1} \end{aligned} \tag{2} $$

#Hopfield神经网络动态方程

$$ \begin{aligned} \frac{du_{xi}}{dt} = - \frac{\partial E}{\partial v_{xi}} = & -A(\sum^n_{i=1}v_{xi}-1)-A(\sum^n_{y=1}v_{yi}-1) \\ & - D(\sum^n_{y=1}v_{xi}d_{xy}v_{y,i+1} \end{aligned} \tag{3} $$

#程序流程

程序流程如图1所示

图1 程序流程图

#核心伪代码

for n in range(num_iter):
    # 利用动态方程计算du
    du = calc_du(V, distance)
    # 由一阶欧拉法更新下一个时间的输入状态（电路的输入电压U）
    U = calc_U(U, du, step)
    # 由sigmoid函数更新下一个时间的输出状态（电路的输出电压V）
    V = calc_V(U, U0)
    # 计算当前网络的能量E
    energys[n] = calc_energy(V, distance)
    # 检查路径的合法性
    route, newV = check_path(V)
    if len(np.unique(route)) == N:
        route.append(route[0])
        dis = calc_distance(route)
        if dis < best_distance:
            H_path = []
            best_distance = dis
            best_route = route
            [H_path.append((route[i], route[i + 1]))
                for i in range(len(route) - 1)]
            print('第{}次迭代找到的次优解距离为：{}，能量为：{}，路径为：'
            .format(n, best_distance, energys[n]))
            [print('[' + str(citys[v][0]) + ',' + str(citys[v][1]) 
            + ']', end=',' if i < len(best_route) - 1 else '\n')
                for i, v in enumerate(best_route)]
if len(H_path) > 0:
    draw_H_and_E(citys, H_path, energys)
else:
    print('没有找到最优解')

#代码运行及测试

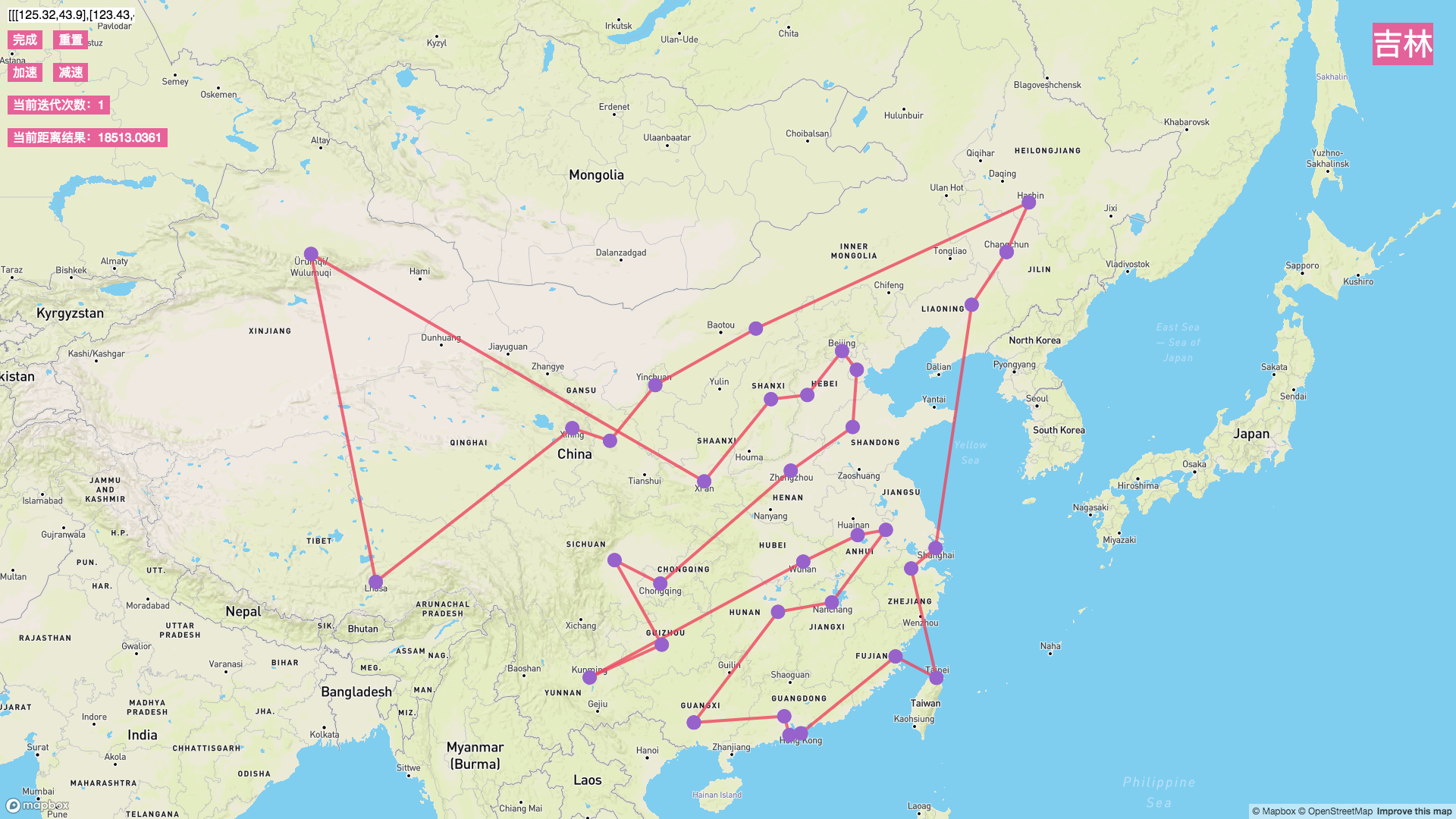
代码运行结果如图2所示.

运行结果图

图2 运行结果图

#结论

34个城市的最终结果为18513.0361公里。
Hopfield神经网络是求解TSP的一种优化网络算法。Hopfield神经网络通过神经动力学来映射生物神经网络，在参数设置合理的情况下，有可能找到真实最优解，比近似算法计算的效果要好。Hopfield神经网络比较依赖初始权值的设置，会受到初始输入状态和输出状态的随机性影响，不一定每一次都可以找到最优解，有可能找到的是不同的次优解。

#参考链接

TSP问题—Hopfield神经网络算法

#附录

#城市坐标

城市坐标表

序号	省份	经度	纬度
01	北京	116.4	39.9
02	天津	117.2	39.12
03	河北	114.52	38.05
04	山西	112.55	37.87
05	内蒙古	111.73	40.83
06	辽宁	123.43	41.8
07	吉林	125.32	43.9
08	黑龙江	126.53	45.8
09	上海	121.47	31.23
10	江苏	118.78	32.07
11	浙江	120.15	30.28
12	安徽	117.25	31.83
13	福建	119.3	26.08
14	江西	115.85	28.68
15	山东	116.98	36.67
16	河南	113.62	34.75
17	湖北	114.3	30.6
18	湖南	112.93	28.23
19	广东	113.27	23.13
20	广西	108.37	22.82
21	海南	108.37	22.82
22	重庆	106.55	29.57
23	四川	104.07	30.67
24	贵州	106.63	26.65
25	云南	102.72	25.05
26	西藏	91.13	29.65
27	陕西	108.93	34.27
28	甘肃	103.82	36.07
29	青海	101.78	36.62
30	宁夏	106.28	38.47
31	新疆	87.62	43.82
32	台北	121.52	25.03
33	香港	114.17	22.28
34	澳门	113.55	22.19

Hopfield神经网络 ↩︎

2018 Computational Intelligence Homework No.6

Contents