#问题描述

小孩分油问题：两个小孩去打油，一人带了一个一斤的空瓶，另一个带了一个七两、一个三两的空瓶。原计划各打一斤油，可是由于所带的钱不够，只好两人合打了一斤油，在回家的路上，两人想平分这一斤油，可是又没有其它工具。试仅用三个瓶子(一斤、七两、三两)精确地分出两个半斤油来。

#算法设计

#选择合适的数据结构表示问题状态

用向量(T, S, Q)表示状态, E表示10斤瓶中的油量, S表示7斤瓶中的油量, Q表示3斤瓶中的油量.

问题的起始状态: (10, 0, 0)

问题的目标状态: (5, 5, 0)

#确定智能算子，用以变化状态的规则

规则表
规则号 规则 解释
1 (T, S, Q) and S<7 and T+S≥7 → (T+S-7, 7, Q) 用10斤瓶油装满7斤瓶
2 (T, S, Q) and Q<3 and T+Q≥3 → (T+Q-3, S, 3) 用10斤瓶油装满3斤瓶
3 (T, S, Q) and T<10 and T+S≥10 → (10, T+S-10, Q) 用7斤瓶油装满10斤瓶
4 (T, S, Q) and Q<3 and S+Q≥3 → (T, S+Q-3, 3) 用7斤瓶油装满3斤瓶
5 (T, S, Q) and T<10 and T+Q≥10 → (10, S, T+Q-10) 用3斤瓶油装满10斤瓶
6 (T, S, Q) and S<7 and S+Q≥7 → (T, 7, S+Q-7) 用3斤瓶油装满7斤瓶
7 (T, S, Q) and T>0 and T+S≤7 → (0, T+S, Q) 10斤瓶油全部倒入7斤瓶
8 (T, S, Q) and T>0 and T+Q≤3 → (0, S, T+Q) 10斤瓶油全部倒入3斤瓶
9 (T, S, Q) and S>0 and T+S≤10 → (T+S, 0, Q) 7斤瓶油全部倒入10斤瓶
10 (T, S, Q) and S>0 and S+Q≤3 → (T, 0, S+Q) 7斤瓶油全部倒入3斤瓶
11 (T, S, Q) and Q>0 and T+Q≤10 → (T+Q, S, 0) 3斤瓶油全部倒入10斤瓶
12 (T, S, Q) and Q>0 and S+Q≤7 → (T, S+Q, 0) 3斤瓶油全部倒入7斤瓶

#确定搜索方法

最基本的搜索方法为深度优先搜索和广度优先搜索, 考虑到本题目存在着无限深度的情况, 故选用广度优先搜索方法来实现.

#程序流程

大体的程序流程如图1所示

图1 程序流程图

#核心伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
while(true) {
  //取出当前队列的头部节点
  currNode = list.shift();

  //队列为空, 搜索失败
  if(currNode == null) {
    break;
  }

  //判断是否为目标状态
  if(checkNode(currNode)) {
    printPath(currNode);
    break;
  }

  //将所有可能的下一步状态加入队列尾部
  pour(currNode);
}

#代码运行及测试

代码运行结果如图2所示, 由于并未对状态进行优化, 首次出现的目标状态在第十层, 有190221 个重复状态, 严重影响了运算速度.

代码运行结果图

图2 代码运行结果图

改进方法是在对目标状态进行搜索的过程中, 对于那些在之前存在过的状态进行剔除, 只保留新状态, 改进后的代码运行结果如图3所示.

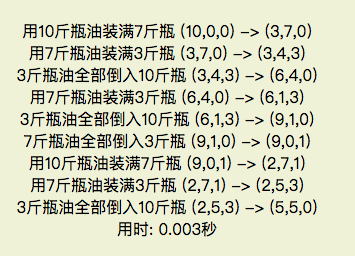
改进后代码运行结果图

图3 改进后代码运行结果图

#结论

从(10, 0, 0)到(5, 5, 0)的分油方法为:

  • 用10斤瓶油装满7斤瓶 (10, 0, 0) -> (3, 7, 0)
  • 用7斤瓶油装满3斤瓶 (3, 7, 0) -> (3, 4, 3)
  • 3斤瓶油全部倒入10斤瓶 (3, 4, 3) -> (6, 4, 0)
  • 用7斤瓶油装满3斤瓶 (6, 4, 0) -> (6, 1, 3)
  • 3斤瓶油全部倒入10斤瓶 (6, 1, 3) -> (9, 1, 0)
  • 7斤瓶油全部倒入3斤瓶 (9, 1, 0) -> (9, 0, 1)
  • 用10斤瓶油装满7斤瓶 (9, 0, 1) -> (2, 7, 1)
  • 用7斤瓶油装满3斤瓶 (2, 7, 1) -> (2, 5, 3)
  • 3斤瓶油全部倒入10斤瓶 (2, 5, 3) -> (5, 5, 0)

如图4所示红色箭头即为分油方法.

图4 分油方法示意图

注:箭头上方数字即为规则号